detectseparation R package is on CRAN Tweet

Pre-fit methods

The pre-fit methods apply on binomial-response generalized liner models such as logit, probit and cloglog regression, and can be directly supplied as fitting methods to the glm() function. They solve the linear programming problems for the detection of separation developed in Konis (2007), using ROI or lpSolveAPI.

For example, the code chunk below checks for data separation for the logistic regression model for the endometrial data set that has been considered in Heinze and Schemper (2002)

library("detectseparation")
data("endometrial", package = "detectseparation")
(endo_sep <- glm(HG ~ NV + PI + EH, data = endometrial,
                 family = binomial("logit"),
                 method = "detect_separation"))
## Implementation: ROI | Solver: lpsolve 
## Separation: TRUE 
## Existence of maximum likelihood estimates
## (Intercept)          NV          PI          EH 
##           0         Inf           0           0 
## 0: finite value, Inf: infinity, -Inf: -infinity

The maximum likelihood estimate for the coefficient of NV is \(+\infty\), while the maximum likelihood estimates for all other parameters are finite. In fact, the maximum likelihood estimates and the corresponding estimated standard errors are

endo_ml <- update(endo_sep, method = "glm.fit")
coef(summary(endo_ml))[, 1:2] + coef(endo_sep)
##               Estimate Std. Error
## (Intercept)  4.3045178 1.63729861
## NV                 Inf        Inf
## PI          -0.0421834 0.04433196
## EH          -2.9026056 0.84555156

Post-fit methods

The post-fit methods apply to models with categorical responses, including binomial-response generalized linear models and multinomial-response models, such as baseline category logits and adjacent category logits models; for example, the models implemented in the brglm2 package. The post-fit methods successively refit the model with increasing number of iteratively reweighted least squares iterations, and monitor the ratio of the estimated standard error for each parameter to what it has been in the first iteration. According to the results in Lesaffre and Albert (1989), divergence of those ratios indicates data separation. For example,

plot(check_infinite_estimates(endo_ml))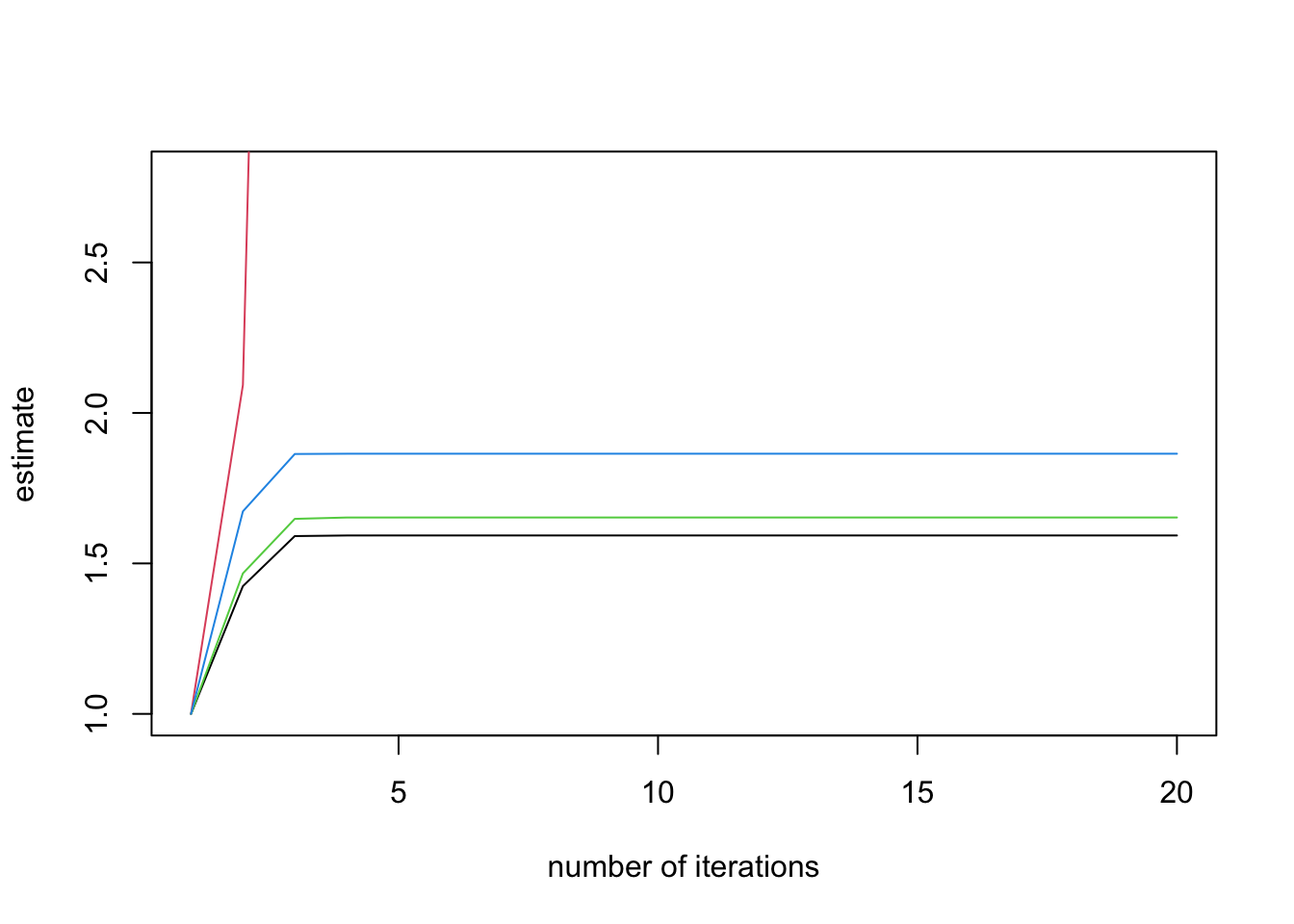

More information

See the package vignettes and the package’s GitHub page for more information.